木盒主机原文链接：http://tecdat.cn/?p=3795
Glmnet是一个通过惩罚最大似然关系拟合广义线性模型的软件包。正则化路径是针对正则化参数λ的值网格处的lasso或Elastic Net（弹性网络）惩罚值计算的 。
该算法非常快，并且可以利用输入矩阵中的稀疏性 x。它适合线性，逻辑和多项式，泊松和Cox回归模型。可以从拟合模型中做出各种预测。
它也可以拟合多元线性回归。
glmnet 解决以下问题
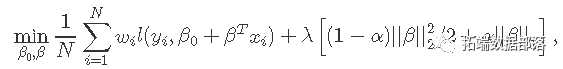
在覆盖整个范围的λ值网格上。这里l（y，η）是观察i的负对数似然贡献；例如对于高斯分布是
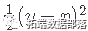
。 _弹性网络_惩罚由α控制，LASSO（α= 1，默认），Ridge（α= 0）。调整参数λ控制惩罚的总强度。
众所周知，岭惩罚使相关预测因子的系数彼此缩小，而套索倾向于选择其中一个而丢弃其他预测因子。_弹性网络_则将这两者混合在一起。
glmnet 算法使用循环坐标下降法，该方法在每个参数固定不变的情况下连续优化目标函数，并反复循环直到收敛，我们的算法可以非常快速地计算求解路径。
代码可以处理稀疏的输入矩阵格式，以及系数的范围约束，还包括用于预测和绘图的方法，以及执行K折交叉验证的功能。
快速开始
首先，我们加载 glmnet 包：
library(glmnet)包中使用的默认模型是高斯线性模型或“最小二乘”。我们加载一组预先创建的数据以进行说明。用户可以加载自己的数据，也可以使用工作空间中保存的数据。
该命令 从此保存的R数据中加载输入矩阵 x 和因向量 y。
我们拟合模型 glmnet。
fit = glmnet(x, y)可以通过执行plot 函数来可视化系数 ：
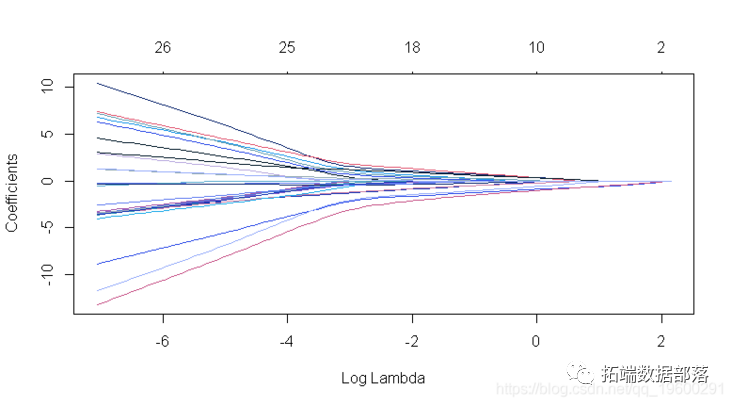
plot(fit)
每条曲线对应一个变量。它显示了当λ变化时，其系数相对于整个系数向量的ℓ1范数的路径。上方的轴表示当前λ处非零系数的数量，这是套索的有效自由度（df）。用户可能还希望对曲线进行注释。这可以通过label = TRUE 在plot命令中进行设置来完成 。
点击标题查阅往期内容
R语言自适应LASSO 多项式回归、二元逻辑回归和岭回归应用分析
01
02
03
04
glmnet 如果我们只是输入对象名称或使用print 函数，则会显示每个步骤的路径 摘要 ：
print(fit)##
## Call: glmnet(x = x, y = y)
##
## Df %Dev Lambda
## [1,] 0 0.0000 1.63000
## [2,] 2 0.0553 1.49000
## [3,] 2 0.1460 1.35000
## [4,] 2 0.2210 1.23000
## [5,] 2 0.2840 1.12000
## [6,] 2 0.3350 1.02000
## [7,] 4 0.3900 0.93300
## [8,] 5 0.4560 0.85000
## [9,] 5 0.5150 0.77500
## [10,] 6 0.5740 0.70600
## [11,] 6 0.6260 0.64300
## [12,] 6 0.6690 0.58600
## [13,] 6 0.7050 0.53400
## [14,] 6 0.7340 0.48700
## [15,] 7 0.7620 0.44300
## [16,] 7 0.7860 0.40400
## [17,] 7 0.8050 0.36800
## [18,] 7 0.8220 0.33500
## [19,] 7 0.8350 0.30600
## [20,] 7 0.8460 0.27800它从左到右显示了非零系数的数量（Df），解释的（零）偏差百分比（%dev）和λ（Lambda）的值。
我们可以在序列范围内获得一个或多个λ处的实际系数：
coef(fit,s=0.1)## 21 x 1 sparse Matrix of class "dgCMatrix"
## 1
## (Intercept) 0.150928
## V1 1.320597
## V2 .
## V3 0.675110
## V4 .
## V5 -0.817412
## V6 0.521437
## V7 0.004829
## V8 0.319416
## V9 .
## V10 .
## V11 0.142499
## V12 .
## V13 .
## V14 -1.059979
## V15 .
## V16 .
## V17 .
## V18 .
## V19 .
## V20 -1.021874还可以使用新的输入数据在特定的λ处进行预测：
predict(fit,newx=nx,s=c(0.1,0.05))## 1 2
## [1,] 4.4641 4.7001
## [2,] 1.7509 1.8513
## [3,] 4.5207 4.6512
## [4,] -0.6184 -0.6764
## [5,] 1.7302 1.8451
## [6,] 0.3565 0.3512
## [7,] 0.2881 0.2662
## [8,] 2.7776 2.8209
## [9,] -3.7016 -3.7773
## [10,] 1.1546 1.1067该函数 glmnet 返回一系列模型供用户选择。交叉验证可能是该任务最简单，使用最广泛的方法。
cv.glmnet 是交叉验证的主要函数。
cv.glmnet 返回一个 cv.glmnet 对象，此处为“ cvfit”，其中包含交叉验证拟合的所有成分的列表。
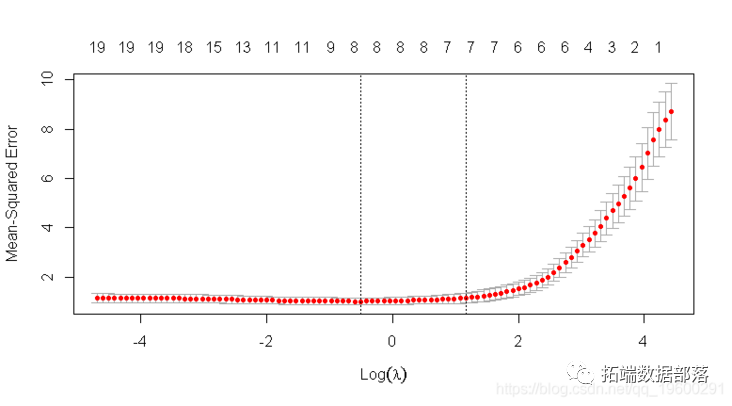
我们可以绘制对象。
它包括交叉验证曲线（红色虚线）和沿λ序列的上下标准偏差曲线（误差线）。垂直虚线表示两个选定的λ。
我们可以查看所选的λ和相应的系数。例如，
cvfit$lambda.min## [1] 0.08307lambda.min 是给出最小平均交叉验证误差的λ值。保存的另一个λ是 lambda.1se，它给出了的模型，使得误差在最小值的一个标准误差以内。我们只需要更换 lambda.min 到lambda.1se 以上。
coef(cvfit, s = "lambda.min")## 21 x 1 sparse Matrix of class "dgCMatrix"
## 1
## (Intercept) 0.14936
## V1 1.32975
## V2 .
## V3 0.69096
## V4 .
## V5 -0.83123
## V6 0.53670
## V7 0.02005
## V8 0.33194
## V9 .
## V10 .
## V11 0.16239
## V12 .
## V13 .
## V14 -1.07081
## V15 .
## V16 .
## V17 .
## V18 .
## V19 .
## V20 -1.04341注意，系数以稀疏矩阵格式表示。原因是沿着正则化路径的解通常是稀疏的，因此使用稀疏格式在时间和空间上更为有效。
可以根据拟合的cv.glmnet 对象进行预测 。让我们看一个示例。
## 1
## [1,] -1.3647
## [2,] 2.5686
## [3,] 0.5706
## [4,] 1.9682
## [5,] 1.4964newx 与新的输入矩阵 s相同，如前所述，是预测的λ值。
线性回归
这里的线性回归是指两个模型系列。一个是 gaussian正态_分布_，另一个是 mgaussian多元正态_分布_。
正态_分布_
假设我们有观测值xi∈Rp并且yi∈R，i = 1，...，N。目标函数是
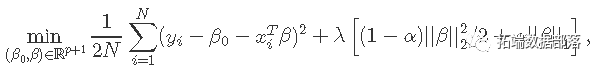
其中λ≥0是复杂度参数，0≤α≤1在岭回归（α=0）和套索LASSO（α=1）之间。
应用坐标下降法解决该问题。具体地说，通过计算βj=β〜j处的梯度和简单的演算，更新为
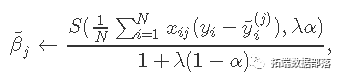
其中
。
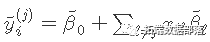
当x 变量标准化为具有单位方差（默认值）时，以上公式适用 。
glmnet 提供各种选项供用户自定义。我们在这里介绍一些常用的选项，它们可以在glmnet 函数中指定 。
alpha表示弹性网混合参数α，范围α∈[0,1]。α=1是套索（默认），α=0是Ridge。weights用于观察权重。每个观察值的默认值为1。nlambda是序列中λ值的数量。默认值为100。lambda可以提供，但通常不提供，程序会构建一个序列。自动生成时，λ序列由lambda.max和 确定lambda.min.ratio。standardize是x在拟合模型序列之前进行变量标准化的逻辑标志 。
例如，我们设置α=0.2，并对后半部分的观测值赋予两倍的权重。为了避免在此处显示太长时间，我们将其设置 nlambda 为20。但是，实际上，建议将λ的数量设置为100（默认值）或更多。
然后我们可以输出glmnet 对象。
print(fit)##
## Call: glmnet(x = x, y = y, weights = c(rep(1, 50), rep(2, 50)), alpha = 0.2, nlambda = 20)
##
## Df %Dev Lambda
## [1,] 0 0.000 7.94000
## [2,] 4 0.179 4.89000
## [3,] 7 0.444 3.01000
## [4,] 7 0.657 1.85000
## [5,] 8 0.785 1.14000
## [6,] 9 0.854 0.70300
## [7,] 10 0.887 0.43300
## [8,] 11 0.902 0.26700
## [9,] 14 0.910 0.16400
## [10,] 17 0.914 0.10100
## [11,] 17 0.915 0.06230
## [12,] 17 0.916 0.03840
## [13,] 19 0.916 0.02360
## [14,] 20 0.916 0.01460
## [15,] 20 0.916 0.00896
## [16,] 20 0.916 0.00552
## [17,] 20 0.916 0.00340这将显示生成对象的调用 fit 以及带有列Df （非零系数的数量）， %dev （解释的偏差百分比）和Lambda （对应的λ值） 的三列矩阵 。
我们可以绘制拟合的对象。
让我们针对log-lambda值标记每个曲线来绘制“拟合”。
这是训练数据中的偏差百分比。我们在这里看到的是，在路径末端时，该值变化不大，但是系数有点“膨胀”。这使我们可以将注意力集中在重要的拟合部分上。
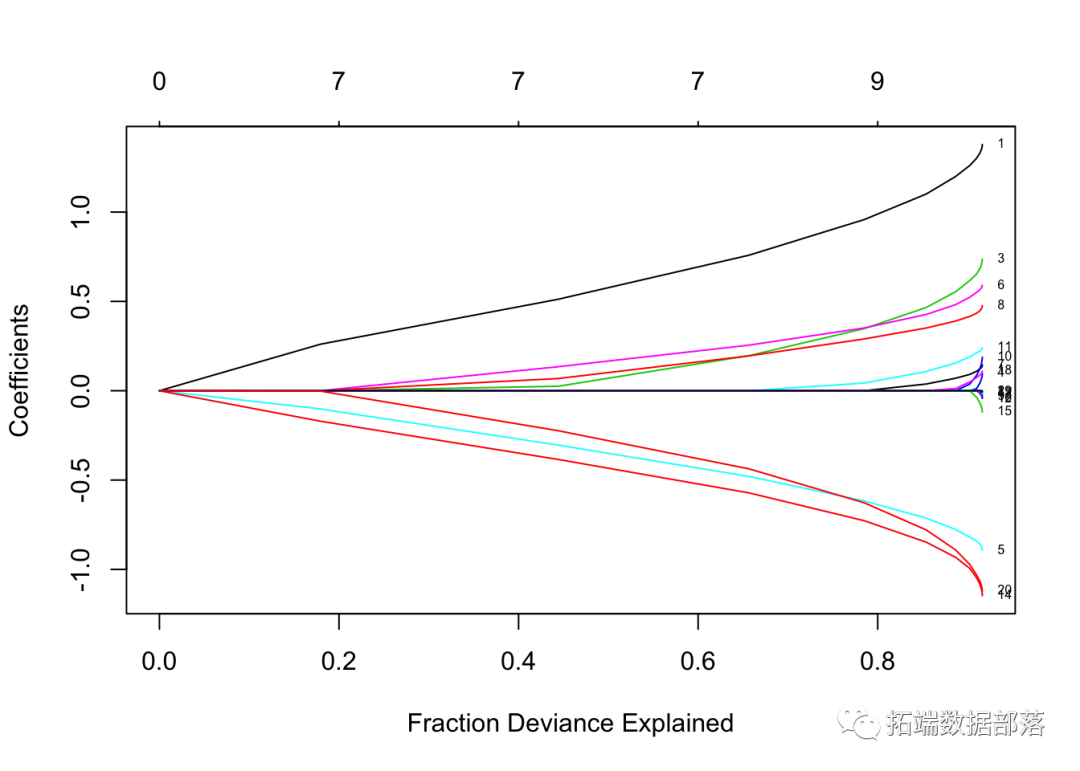
我们可以提取系数并在某些特定值的情况下进行预测。两种常用的选项是：
s指定进行提取的λ值。exact指示是否需要系数的精确值。
一个简单的例子是：
## 21 x 2 sparse Matrix of class "dgCMatrix"
## 1 1
## (Intercept) 0.19657 0.199099
## V1 1.17496 1.174650
## V2 . .
## V3 0.52934 0.531935
## V4 . .
## V5 -0.76126 -0.760959
## V6 0.46627 0.468209
## V7 0.06148 0.061927
## V8 0.38049 0.380301
## V9 . .
## V10 . .
## V11 0.14214 0.143261
## V12 . .
## V13 . .
## V14 -0.91090 -0.911207
## V15 . .
## V16 . .
## V17 . .
## V18 . 0.009197
## V19 . .
## V20 -0.86099 -0.863117左列是，exact = TRUE 右列是 FALSE。从上面我们可以看到，0.01不在序列中，因此尽管没有太大差异，但还是有一些差异。如果没有特殊要求，则线性插补就足够了。
用户可以根据拟合的对象进行预测。除中的选项外 coef，主要参数是 newx的新值矩阵 x。type 选项允许用户选择预测类型：*“链接”给出拟合值
- 因变量与正态分布的“链接”相同。
- “系数”计算值为的系数
s
例如，
## 1
## [1,] -0.9803
## [2,] 2.2992
## [3,] 0.6011
## [4,] 2.3573
## [5,] 1.7520给出在λ=0.05时前5个观测值的拟合值。如果提供的多个值， s 则会生成预测矩阵。
用户可以自定义K折交叉验证。除所有 glmnet 参数外， cv.glmnet 还有特殊的参数，包括 nfolds （次数）， foldid （用户提供的次数）， type.measure（用于交叉验证的损失）：*“ deviance”或“ mse”
- “ mae”使用平均绝对误差
举个例子，
cvfit = cv.glmnet(x, y, type.measure = "mse", nfolds = 20)根据均方误差标准进行20折交叉验证。
并行计算也受 cv.glmnet。为我们在这里给出一个简单的比较示例。
system.time(cv.glmnet(X, Y))## user system elapsed
## 3.591 0.103 3.724system.time(cv.glmnet(X, Y, parallel = TRUE))## user system elapsed
## 4.318 0.391 2.700从上面的建议可以看出，并行计算可以大大加快计算过程。
- “ lambda.min”：达到最小MSE的λ。
cvfit$lambda.min## [1] 0.08307## 21 x 1 sparse Matrix of class "dgCMatrix"
## 1
## (Intercept) 0.14936
## V1 1.32975
## V2 .
## V3 0.69096
## V4 .
## V5 -0.83123
## V6 0.53670
## V7 0.02005
## V8 0.33194
## V9 .
## V10 .
## V11 0.16239
## V12 .
## V13 .
## V14 -1.07081
## V15 .
## V16 .
## V17 .
## V18 .
## V19 .
## V20 -1.04341在这里，我们使用相同的k折，为α选择一个值。
将它们全部放置在同一绘图上：
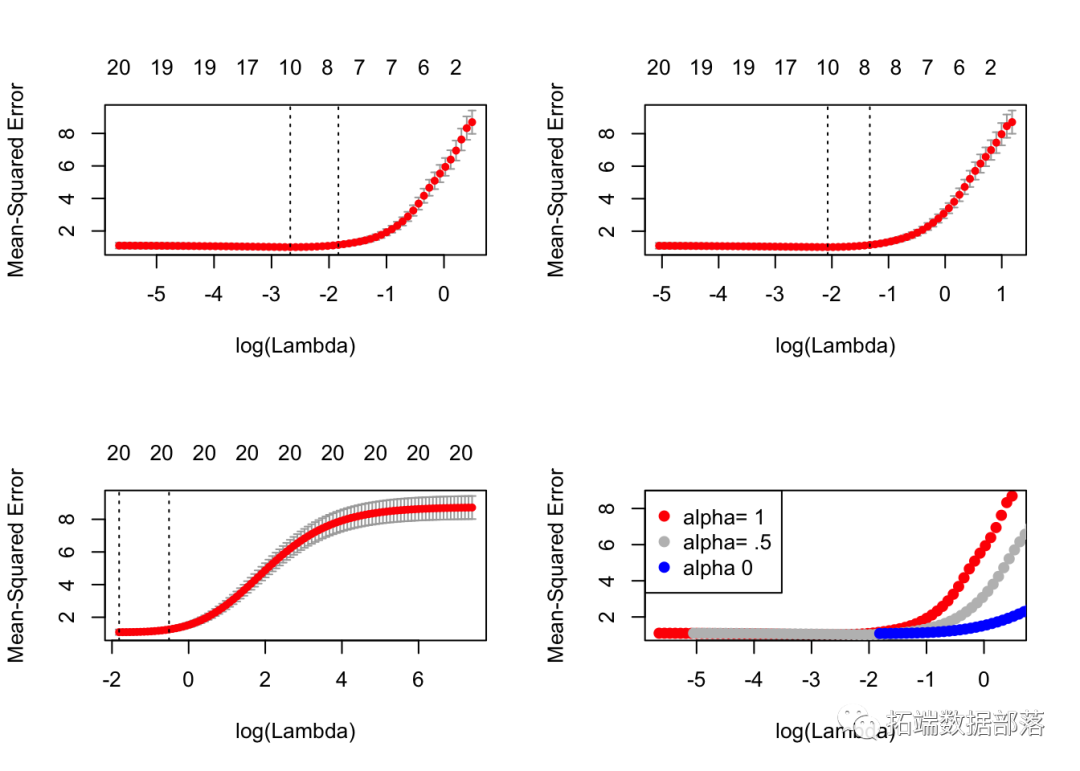
我们看到lasso（alpha=1）在这里表现最好。
系数上下限
假设我们要拟合我们的模型，但将系数限制为大于-0.7且小于0.5。这可以通过upper.limits 和 lower.limits 参数实现 ：
通常，我们希望系数为正，因此我们只能lower.limit 将其设置 为0。
惩罚因素
此参数允许用户将单独的惩罚因子应用于每个系数。每个参数的默认值为1，但可以指定其他值。特别是，任何penalty.factor 等于零的变量 都不会受到惩罚
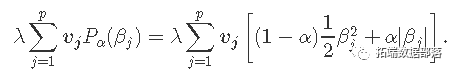
在许多情况下，某些变量可能是重要，我们希望一直保留它们，这可以通过将相应的惩罚因子设置为0来实现：
我们从标签中看到惩罚因子为0的三个变量始终保留在模型中，而其他变量遵循典型的正则化路径并最终缩小为0。
自定义图
有时，尤其是在变量数量很少的情况下，我们想在图上添加变量标签。
我们首先生成带有10个变量的一些数据，然后，我们拟合glmnet模型，并绘制标准图。
我们希望用变量名标记曲线。在路径的末尾放置系数的位置。
多元正态
使用family = "mgaussian" option 获得多元正态分布glmnet。
显然，顾名思义，y不是向量，而是矩阵。结果，每个λ值的系数也是一个矩阵。
在这里，我们解决以下问题：
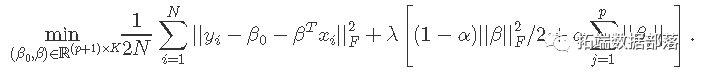
这里，βj是p×K系数矩阵β的第j行，对于单个预测变量xj，我们用每个系数K向量βj的组套索罚分代替每个单一系数的绝对罚分。
我们使用预先生成的一组数据进行说明。
我们拟合数据，并返回对象“ mfit”。
mfit = glmnet(x, y, family = "mgaussian")如果为 standardize.response = TRUE，则将因变量标准化。
为了可视化系数，我们使用 plot 函数。
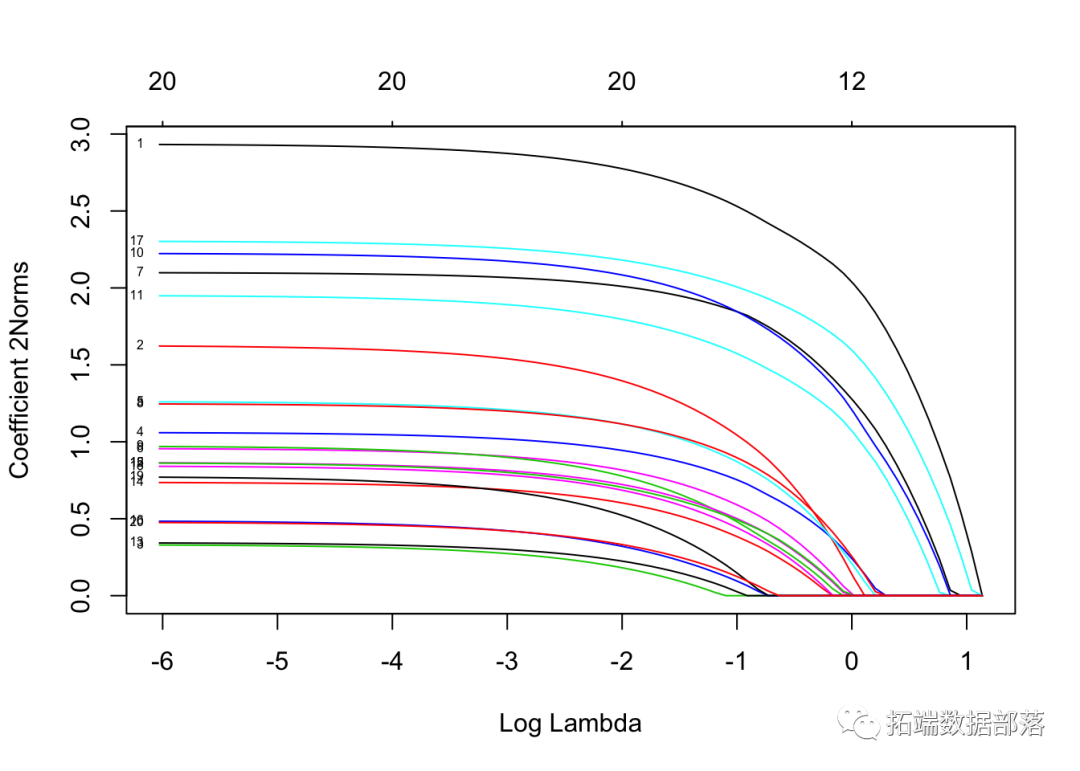
注意我们设置了 type.coef = "2norm"。在此设置下，每个变量绘制一条曲线，其值等于ℓ2范数。默认设置为 type.coef = "coef"，其中为每个因变量创建一个系数图。
通过使用该函数coef ，我们可以提取要求的λ值的系数， 并通过进行预测 。
## , , 1
##
## y1 y2 y3 y4
## [1,] -4.7106 -1.1635 0.6028 3.741
## [2,] 4.1302 -3.0508 -1.2123 4.970
## [3,] 3.1595 -0.5760 0.2608 2.054
## [4,] 0.6459 2.1206 -0.2252 3.146
## [5,] -1.1792 0.1056 -7.3353 3.248
##
## , , 2
##
## y1 y2 y3 y4
## [1,] -4.6415 -1.2290 0.6118 3.780
## [2,] 4.4713 -3.2530 -1.2573 5.266
## [3,] 3.4735 -0.6929 0.4684 2.056
## [4,] 0.7353 2.2965 -0.2190 2.989
## [5,] -1.2760 0.2893 -7.8259 3.205预测结果保存在三维数组中，其中前两个维是每个因变量的预测矩阵，第三个维表示因变量。
我们还可以进行k折交叉验证。
我们绘制结果 cv.glmnet 对象“ cvmfit”。
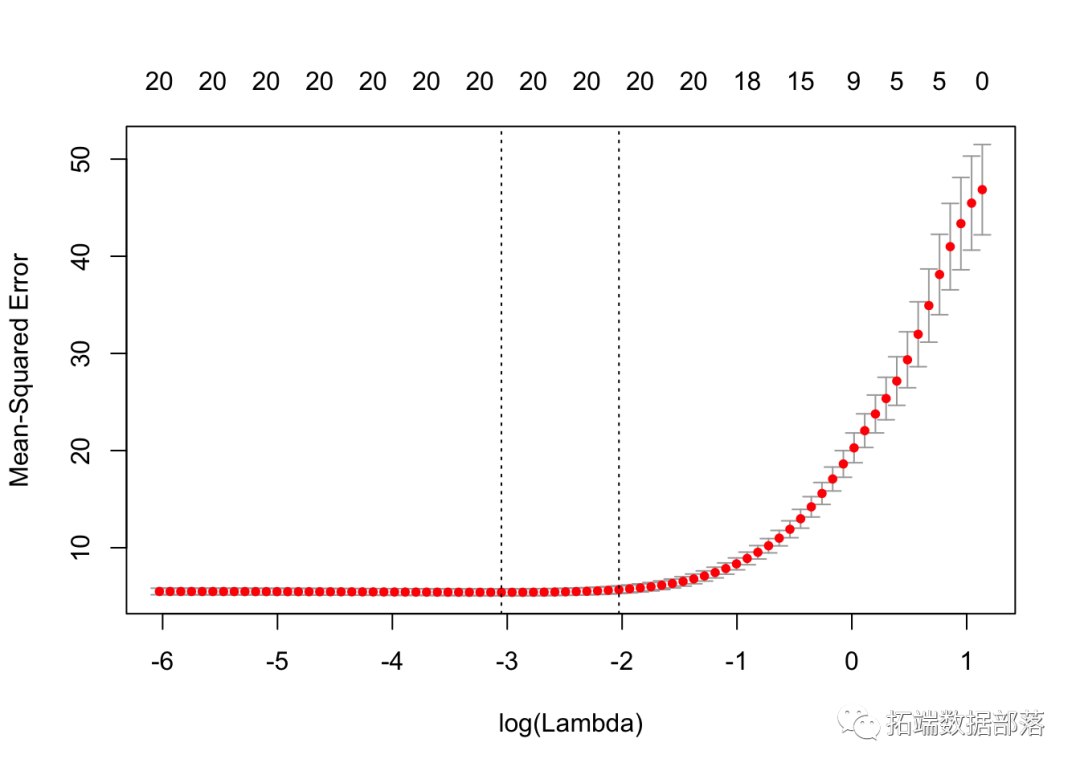
显示选定的λ最佳值
cvmfit$lambda.min## [1] 0.04732cvmfit$lambda.1se## [1] 0.1317逻辑回归
当因变量是分类的时，逻辑回归是另一个广泛使用的模型。如果有两个可能的结果，则使用二项式分布，否则使用多项式。
二项式模型
对于二项式模型，假设因变量的取值为G = {1,2} 。表示yi = I（gi = 1）。我们建模
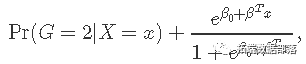
可以用以下形式写
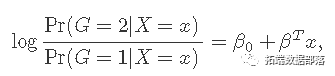
惩罚逻辑回归的目标函数使用负二项式对数似然
我们的算法使用对数似然的二次逼近，然后对所得的惩罚加权最小二乘问题进行下降。这些构成了内部和外部循环。
出于说明目的，我们 从数据文件加载预生成的输入矩阵 x 和因变量 y。
对于二项式逻辑回归，因变量y可以是两个级别的因子，也可以是计数或比例的两列矩阵。
glmnet 二项式回归的其他可选参数与正态分布的参数 几乎相同。不要忘记将family 选项设置 为“ binomial”。
fit = glmnet(x, y, family = "binomial")像以前一样，我们可以输出和绘制拟合的对象，提取特定λ处的系数，并进行预测。
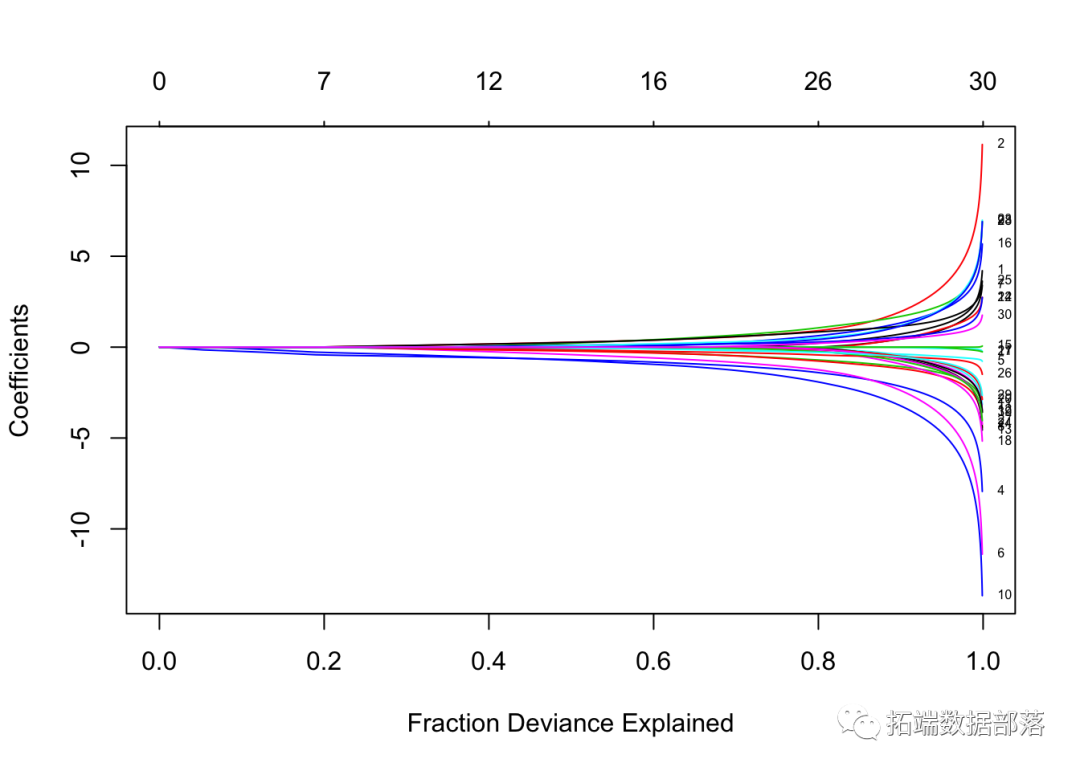
逻辑回归略有不同，主要体现在选择上 type。“链接”和“因变量”不等价，“类”仅可用于逻辑回归。总之，*“链接”给出了线性预测变量
- “因变量”给出合适的概率
- “类别”产生对应于最大概率的类别标签。
- “系数”计算值为的系数
s
在下面的示例中，我们在λ=0.05,0.01的情况下对类别标签进行了预测。
## 1 2
## [1,] "0" "0"
## [2,] "1" "1"
## [3,] "1" "1"
## [4,] "0" "0"
## [5,] "1" "1"对于逻辑回归，type.measure：
- “偏差”使用实际偏差。
- “ mae”使用平均绝对误差。
- “class”给出错误分类错误。
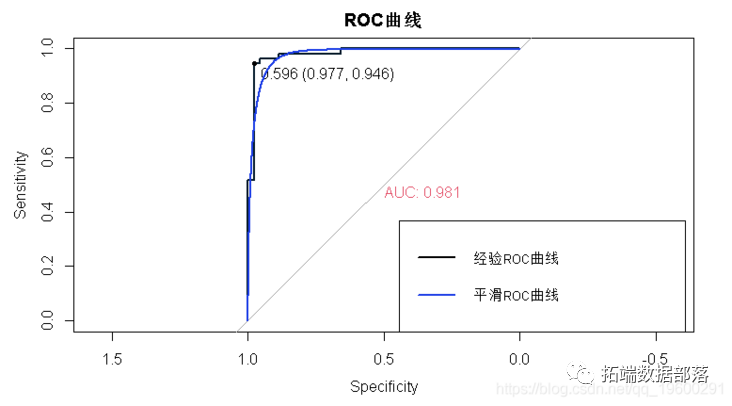
- “ auc”（仅适用于两类逻辑回归）给出了ROC曲线下的面积。
例如，
它使用分类误差作为10倍交叉验证的标准。
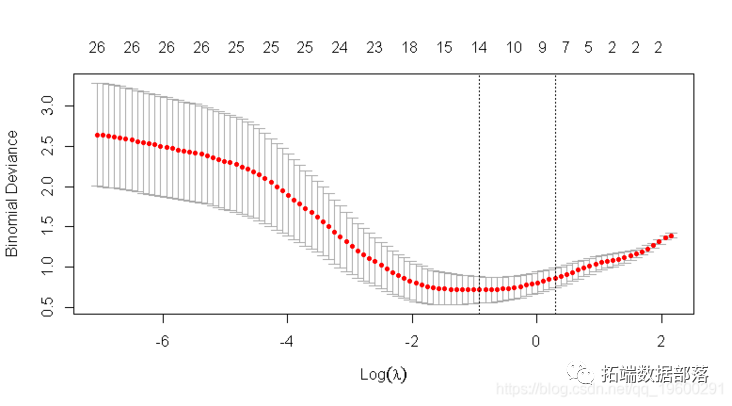
我们绘制对象并显示λ的最佳值。
cvfit$lambda.min## [1] 0.01476cvfit$lambda.1se## [1] 0.02579coef 并且 predict 类似于正态分布案例，因此我们省略了细节。我们通过一些例子进行回顾。
## 31 x 1 sparse Matrix of class "dgCMatrix"
## 1
## (Intercept) 0.24371
## V1 0.06897
## V2 0.66252
## V3 -0.54275
## V4 -1.13693
## V5 -0.19143
## V6 -0.95852
## V7 .
## V8 -0.56529
## V9 0.77454
## V10 -1.45079
## V11 -0.04363
## V12 -0.06894
## V13 .
## V14 .
## V15 .
## V16 0.36685
## V17 .
## V18 -0.04014
## V19 .
## V20 .
## V21 .
## V22 0.20882
## V23 0.34014
## V24 .
## V25 0.66310
## V26 -0.33696
## V27 -0.10570
## V28 0.24318
## V29 -0.22445
## V30 0.11091如前所述，此处返回的结果仅针对因子因变量的第二类。
## 1
## [1,] "0"
## [2,] "1"
## [3,] "1"
## [4,] "0"
## [5,] "1"
## [6,] "0"
## [7,] "0"
## [8,] "0"
## [9,] "1"
## [10,] "1"多项式模型
对于多项式模型，假设因变量变量的K级别为G = {1,2，…，K}。在这里我们建模
设Y为N×K指标因变量矩阵，元素yiℓ= I（gi =ℓ）。然后弹性网惩罚的负对数似然函数变为
β是系数的p×K矩阵。βk指第k列（对于结果类别k），βj指第j行（变量j的K个系数的向量）。最后一个惩罚项是||βj|| q ，我们对q有两个选择：q∈{1,2}。当q = 1时，这是每个参数的套索惩罚。当q = 2时，这是对特定变量的所有K个系数的分组套索惩罚，这使它们在一起全为零或非零。
对于多项式情况，用法类似于逻辑回归，我们加载一组生成的数据。
glmnet 除少数情况外，多项式逻辑回归中的可选参数 与二项式回归基本相似。
多项式回归的一个特殊选项是 type.multinomial，如果允许，则允许使用分组的套索罚分 type.multinomial = "grouped"。这将确保变量的多项式系数全部一起输入或输出，就像多元因变量一样。
我们绘制结果。
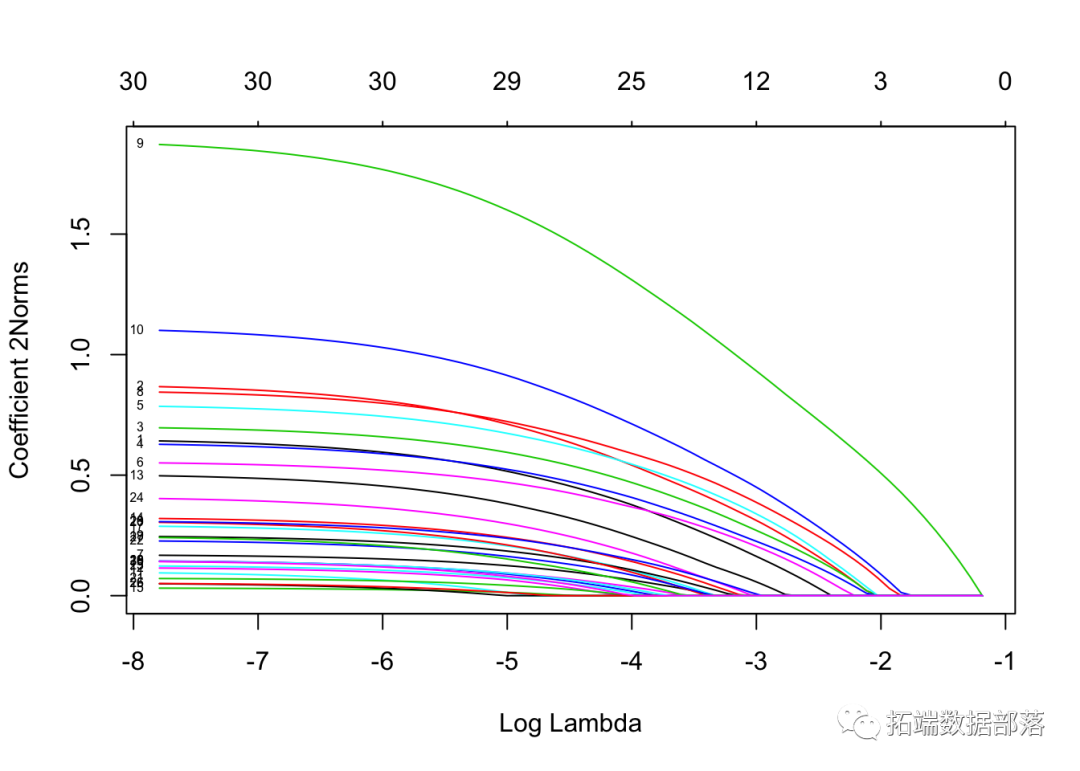
我们还可以进行交叉验证并绘制返回的对象。
预测最佳选择的λ：
## 1
## [1,] "3"
## [2,] "2"
## [3,] "2"
## [4,] "1"
## [5,] "1"
## [6,] "3"
## [7,] "3"
## [8,] "1"
## [9,] "1"
## [10,] "2"泊松模型
Poisson回归用于在假设Poisson误差的情况下对计数数据进行建模，或者在均值和方差成比例的情况下使用非负数据进行建模。泊松也是指数分布族的成员。我们通常以对数建模：。
给定观测值的对数似然
和以前一样，我们优化了惩罚对数：
Glmnet使用外部牛顿循环和内部加权最小二乘循环（如逻辑回归）来优化此标准。
首先，我们加载一组泊松数据。
再次，绘制系数。
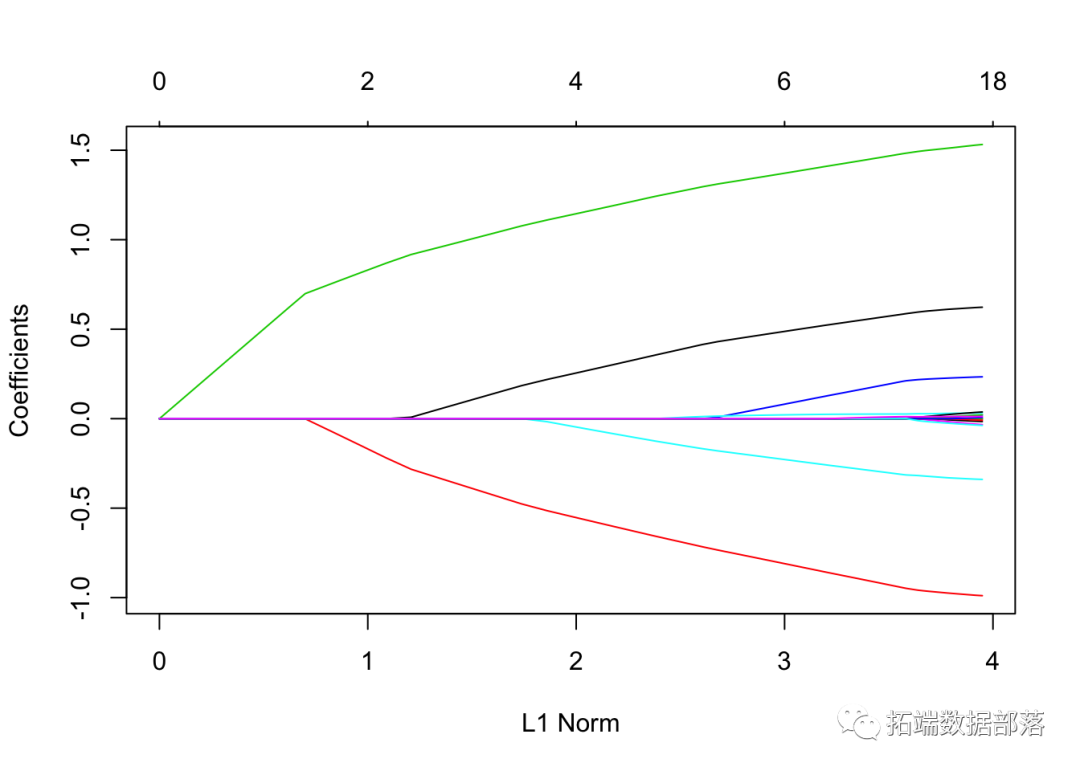
像以前一样，我们可以 分别使用coef 和 提取系数并在特定的λ处进行预测 predict。
例如，我们可以
## 21 x 1 sparse Matrix of class "dgCMatrix"
## 1
## (Intercept) 0.61123
## V1 0.45820
## V2 -0.77061
## V3 1.34015
## V4 0.04350
## V5 -0.20326
## V6 .
## V7 .
## V8 .
## V9 .
## V10 .
## V11 .
## V12 0.01816
## V13 .
## V14 .
## V15 .
## V16 .
## V17 .
## V18 .
## V19 .
## V20 .## 1 2
## [1,] 2.4944 4.4263
## [2,] 10.3513 11.0586
## [3,] 0.1180 0.1782
## [4,] 0.9713 1.6829
## [5,] 1.1133 1.9935我们还可以使用交叉验证来找到最佳的λ，从而进行推断。
选项几乎与正态族相同，不同之处在于 type.measure ，“ mse”代表均方误差，“ mae”代表均值绝对误差。
我们可以绘制 cv.glmnet 对象。
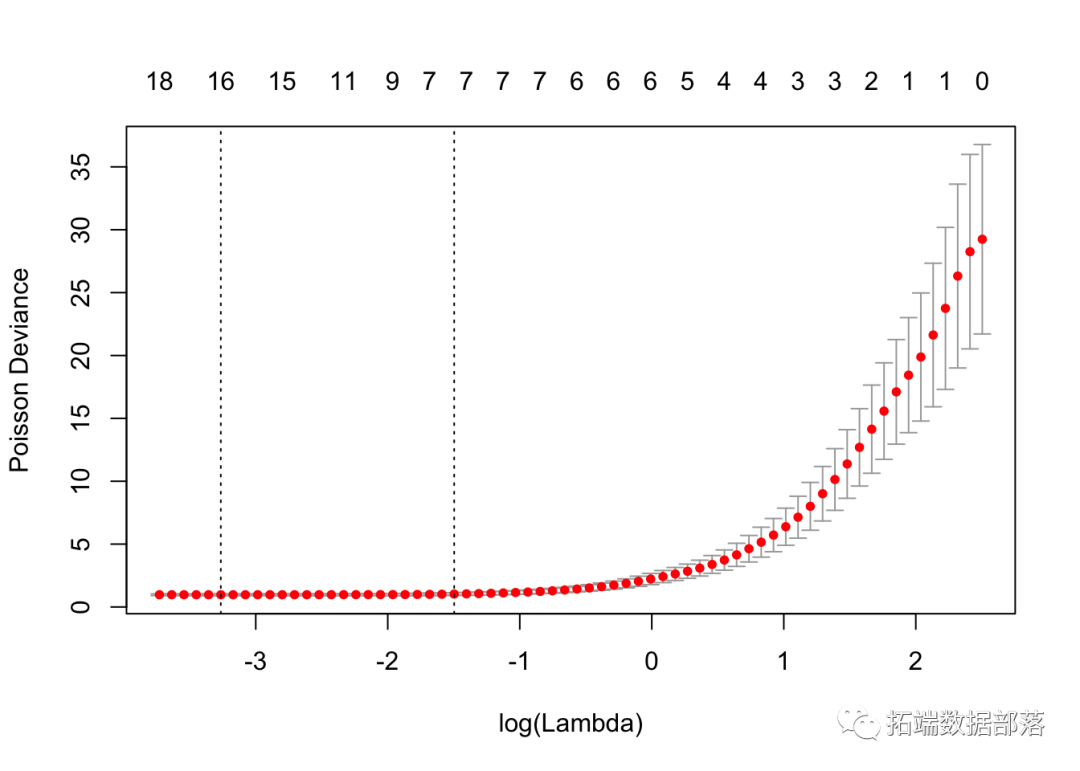
我们还可以显示最佳的λ和相应的系数。
## 21 x 2 sparse Matrix of class "dgCMatrix"
## 1 2
## (Intercept) 0.031263 0.18570
## V1 0.619053 0.57537
## V2 -0.984550 -0.93212
## V3 1.525234 1.47057
## V4 0.231591 0.19692
## V5 -0.336659 -0.30469
## V6 0.001026 .
## V7 -0.012830 .
## V8 . .
## V9 . .
## V10 0.015983 .
## V11 . .
## V12 0.030867 0.02585
## V13 -0.027971 .
## V14 0.032750 .
## V15 -0.005933 .
## V16 0.017506 .
## V17 . .
## V18 0.004026 .
## V19 -0.033579 .
## V20 0.012049 0.00993Cox模型
Cox比例风险模型通常用于研究预测变量与生存时间之间的关系。
Cox比例风险回归模型，它不是直接考察 与X的关系，而是用 作为因变量，模型的基本形式为：
式中， 为自变量的偏回归系数，它是须从样本数据作出估计的参数； 是当X向量为0时， 的基准危险率，它是有待于从样本数据作出估计的量。简称为Cox回归模型。
由于Cox回归模型对 未作任何假定，因此Cox回归模型在处理问题时具有较大的灵活性；另一方面，在许多情况下，我们只需估计出参数 (如因素分析等)，即使在 未知的情况下，仍可估计出参数 。这就是说，Cox回归模型由于含有 ，因此它不是完全的参数模型，但仍可根据公式(1)作出参数 的估计，故Cox回归模型属于半参数模型。
公式可以转化为：
我们使用一组预先生成的样本数据。用户可以加载自己的数据并遵循类似的过程。在这种情况下，x必须是协变量值的n×p矩阵-每行对应一个患者，每列对应一个协变量。y是一个n×2矩阵。
## time status
## [1,] 1.76878 1
## [2,] 0.54528 1
## [3,] 0.04486 0
## [4,] 0.85032 0
## [5,] 0.61488 1Surv 包中的 函数 survival 可以创建这样的矩阵。
我们计算默认设置下的求解路径。
绘制系数。
提取特定值λ处的系数。
## 30 x 1 sparse Matrix of class "dgCMatrix"
## 1
## V1 0.37694
## V2 -0.09548
## V3 -0.13596
## V4 0.09814
## V5 -0.11438
## V6 -0.38899
## V7 0.24291
## V8 0.03648
## V9 0.34740
## V10 0.03865
## V11 .
## V12 .
## V13 .
## V14 .
## V15 .
## V16 .
## V17 .
## V18 .
## V19 .
## V20 .
## V21 .
## V22 .
## V23 .
## V24 .
## V25 .
## V26 .
## V27 .
## V28 .
## V29 .
## V30 .函数 cv.glmnet 可用于计算Cox模型的k折交叉验证。
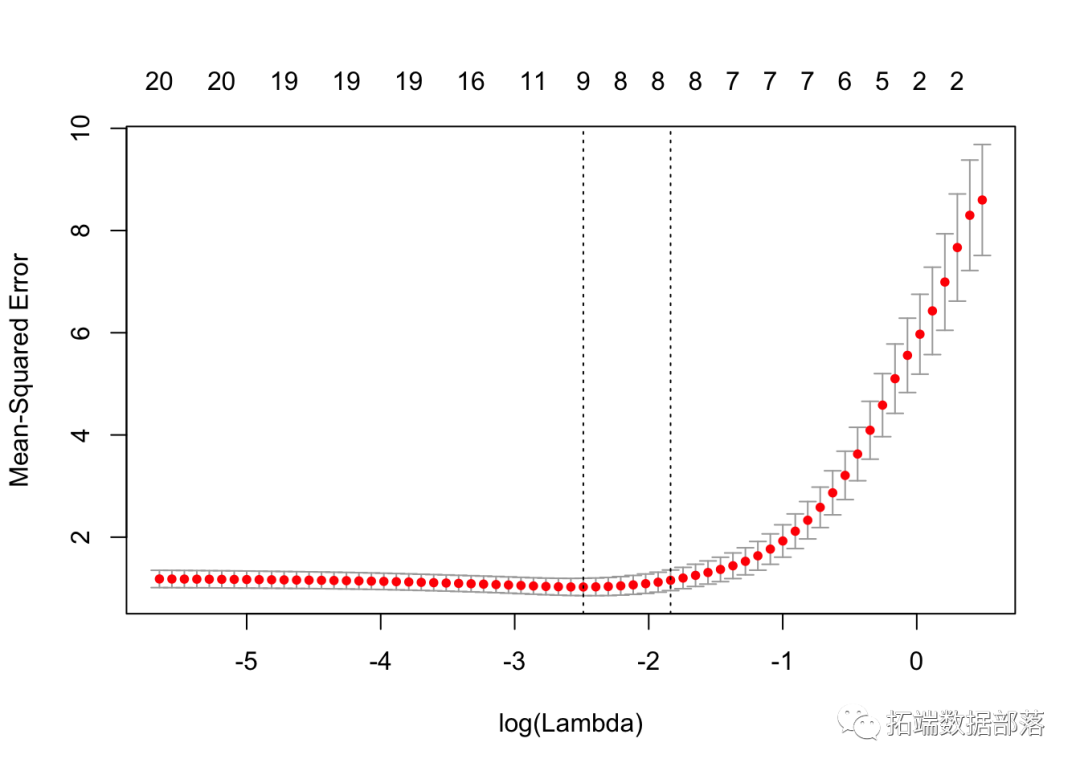
拟合后，我们可以查看最佳λ值和交叉验证的误差图，帮助评估我们的模型。
如前所述，图中的左垂直线向我们显示了CV误差曲线达到最小值的位置。右边的垂直线向我们展示了正则化的模型，其CV误差在最小值的1个标准偏差之内。我们还提取了最优λ。
cvfit$lambda.min## [1] 0.01594cvfit$lambda.1se## [1] 0.04869我们可以检查模型中的协变量并查看其系数。
index.min## [1] 0.491297 -0.174601 -0.218649 0.175112 -0.186673 -0.490250 0.335197
## [8] 0.091587 0.450169 0.115922 0.017595 -0.018365 -0.002806 -0.001423
## [15] -0.023429 0.001688 -0.008236coef.min## 30 x 1 sparse Matrix of class "dgCMatrix"
## 1
## V1 0.491297
## V2 -0.174601
## V3 -0.218649
## V4 0.175112
## V5 -0.186673
## V6 -0.490250
## V7 0.335197
## V8 0.091587
## V9 0.450169
## V10 0.115922
## V11 .
## V12 .
## V13 0.017595
## V14 .
## V15 .
## V16 .
## V17 -0.018365
## V18 .
## V19 .
## V20 .
## V21 -0.002806
## V22 -0.001423
## V23 .
## V24 .
## V25 -0.023429
## V26 .
## V27 0.001688
## V28 .
## V29 .
## V30 -0.008236稀疏矩阵
我们的程序包支持稀疏的输入矩阵，该矩阵可以高效地存储和操作大型矩阵，但只有少数几个非零条目。
我们加载一组预先创建的样本数据。
加载100 * 20的稀疏矩阵和 y因向量。
## [1] "dgCMatrix"
## attr(,"package")
## [1] "Matrix"我们可以像以前一样拟合模型。
fit = glmnet(x, y)进行交叉验证并绘制结果对象。
预测新输入矩阵 。例如，
## 1
## [1,] 0.3826
## [2,] -0.2172
## [3,] -1.6622
## [4,] -0.4175
## [5,] -1.3941参考文献
Jerome Friedman, Trevor Hastie and Rob Tibshirani. (2008).
Regularization Paths for Generalized Linear Models via Coordinate Descent
本文选自《r语言中对LASSO回归，Ridge岭回归和弹性网络Elastic Net模型实现》。
未经允许不得转载：木盒主机 » r语言中对LASSO回归，Ridge岭回归和弹性网络Elastic Net模型实现|附代码数据
搬瓦工VPS最新优惠码 搬瓦工最高优惠6.81%优惠码 promo coupon code 
RackNerd：美国VPS 黑五优惠折扣 1核768RAM $10.28/年+神秘盒子 可随机减免金额
10G.BIZ【年终钜惠】美国/日本/韩国/香港独立服务器 秒杀仅24起，站群仅需99，三网CN2GIA五折抢购。CERA洛杉矶云服务器仅2.4起
2022年RackNerd 美国VPS促销：4TB月流量11.88美元/年，支持支付宝，老优惠$9.89美元/年