数学建模主成分分析法matlab_主成分分析法建模

前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽默，忍不住分享一下给大家，(ﾉ´▽｀)ﾉ♪-》点击这里->一个宝藏级人工智能教程网站。

文章目录

• • Ⅰ.主成分分析：
  • • 主成分与原始变量之间的关系：
    • PCA降维：
  • Ⅱ.SPSS主成分分析的步骤如下：
  • • A.求指标对应的系数
    • 1.方差图与成分矩阵：
    • 2.指标系数=成分矩阵中的数据/sqrt(主成分相对应的特征值)
    • 3.主成分的对应的系数=特征值方差的占比/所有特征值方差占比的总和
    • 4.采用excel的公式计算指标系数
    • 5.数据的归一化处理
    • • a.操作如下：
      • b.得到归一化后的数据：
      • c.然后将数据导入excel进行得分项的输出并排序：
    • B.附spss的免安装文件地址：

Ⅰ.主成分分析：

​ 主成分分析（Principal Component Analysis，PCA）， 将多个变量通过线性变换以选出较少个数重要变量的一种 多元统计分析方法。

主成分与原始变量之间的关系：

​ （1）主成分保留了原始变量绝大多数信息。

​ （2）主成分的个数大大少于原始变量的数目。

​ （3）各个主成分之间互不相关。

​ （4）每个主成分都是原始变量的线性组合。

PCA降维：

​ 假设我们所讨论的实际问题中，有p个指标，我们把这 p个指标看作p个随机变量，记为X1，X2，…，Xp，主 成分分析就是要把这p个指标的问题，转变为讨论p个 指标的线性组合的问题，而这些新的指标F1，F2，…， Fk(k≤p），按照保留主要信息量的原则充分反映原指标 的信息，并且相互独立。

​ 这种由讨论多个指标降为少数几个综合指标的过程在 数学上就叫做降维。主成分分析通常的做法是，寻求 原指标的线性组合Fi。

Ⅱ.SPSS主成分分析的步骤如下：

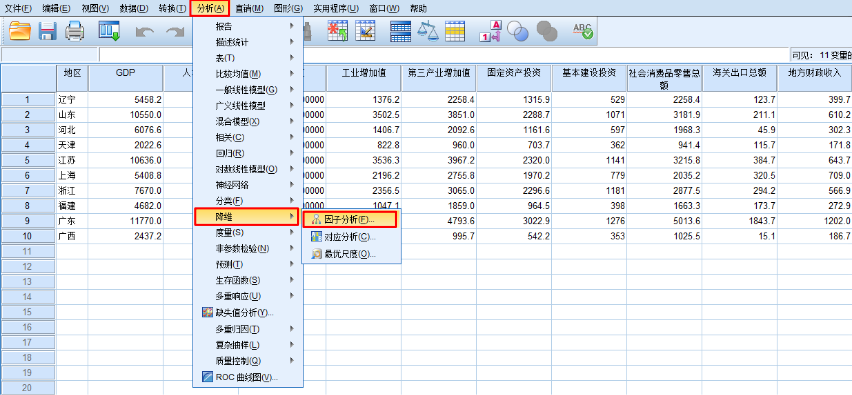
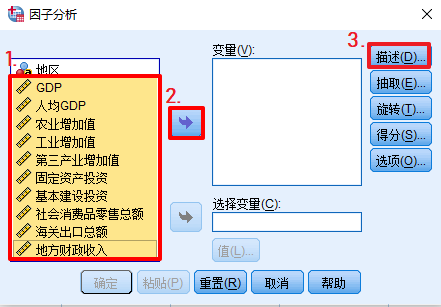
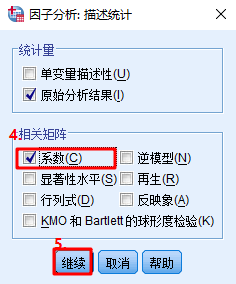
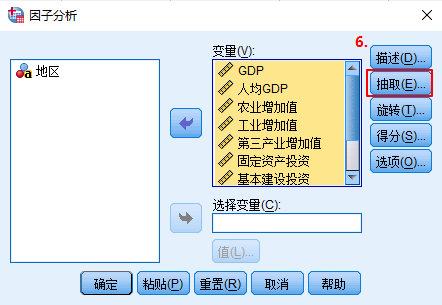
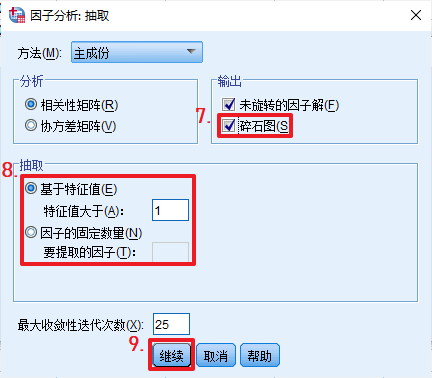
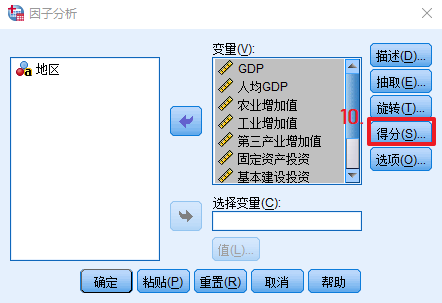
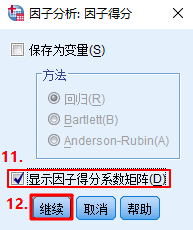
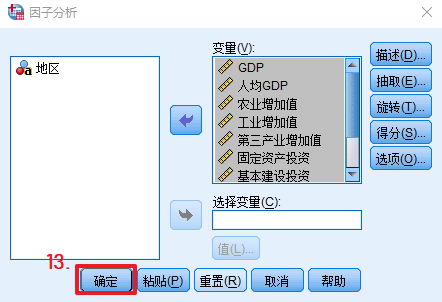
A.求指标对应的系数

1.方差图与成分矩阵：

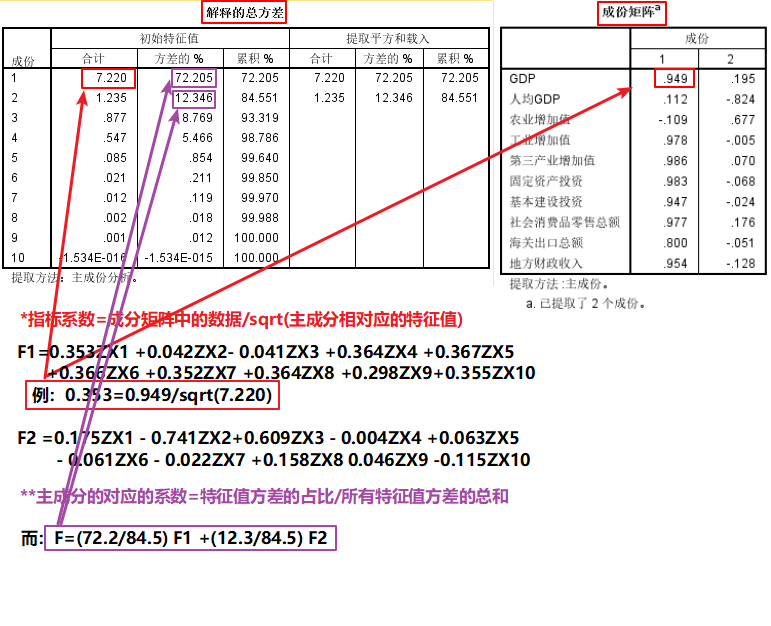
2.指标系数=成分矩阵中的数据/sqrt(主成分相对应的特征值)

F1=0.353ZX1 +0.042ZX2- 0.041ZX3 +0.364ZX4 +0.367ZX5 +0.366ZX6 +0.352ZX7 +0.364ZX8 +0.298ZX9+0.355ZX10

F2 =0.175ZX1 – 0.741ZX2+0.609ZX3 – 0.004ZX4 +0.063ZX5- 0.061ZX6 – 0.022ZX7 +0.158ZX8 0.046ZX9 -0.115ZX10

(注：ZX1,ZX2,…ZX10均为归一化之后处理的数据，而不是原数据表格中的数值，目的在于统一不同的量纲。)

3.主成分的对应的系数=特征值方差的占比/所有特征值方差占比的总和

F=(72.2/84.5) F1 +(12.3/84.5) F2

4.采用excel的公式计算指标系数

将成分矩阵的数据列导入excel表格。

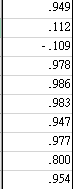
然后通过Excel命令：

​ =A1/sqrt(主成分的特征值)

得到结果：

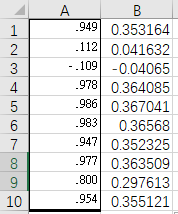
5.数据的归一化处理

a.操作如下：

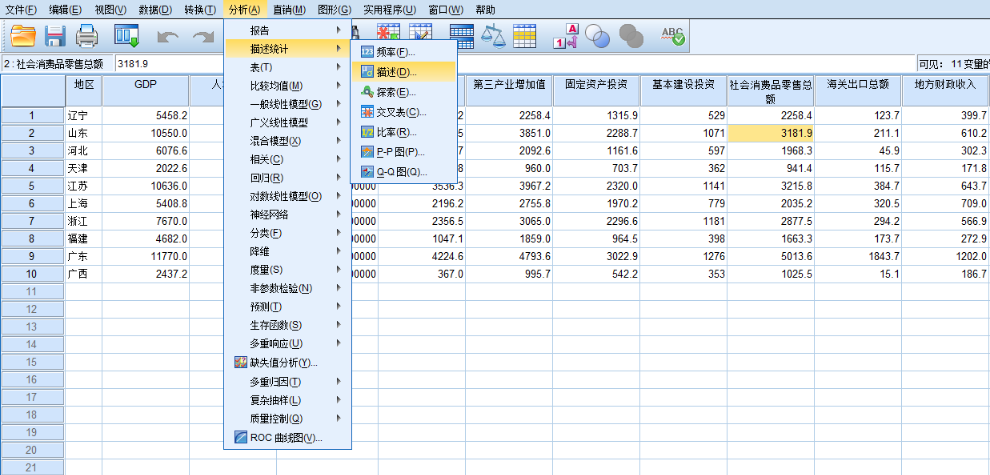
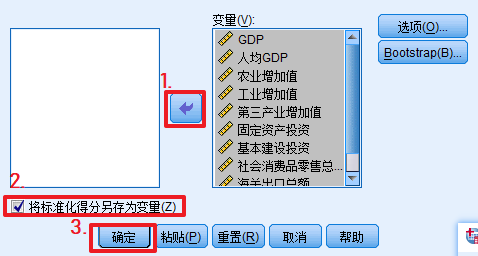
b.得到归一化后的数据：

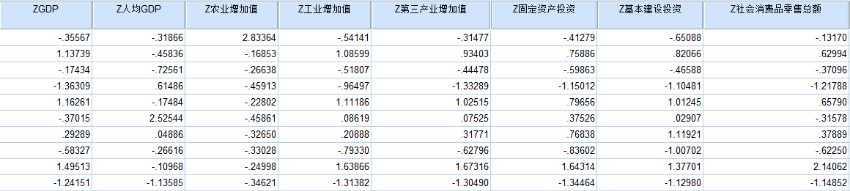
c.然后将数据导入excel进行得分项的输出并排序：

​ 通过F1的计算公式得到F1标准下的测评得分。

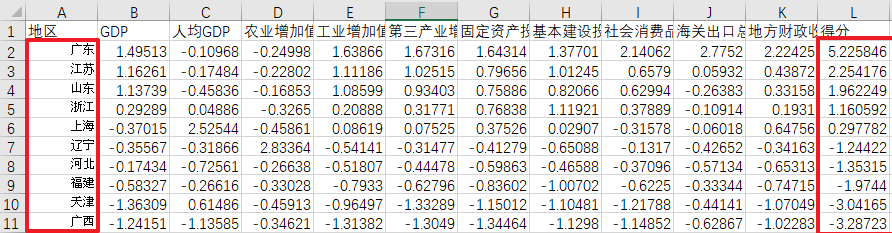
​ F2同理可得；

​ 最终根据F的计算式得到最终测评得分排序。

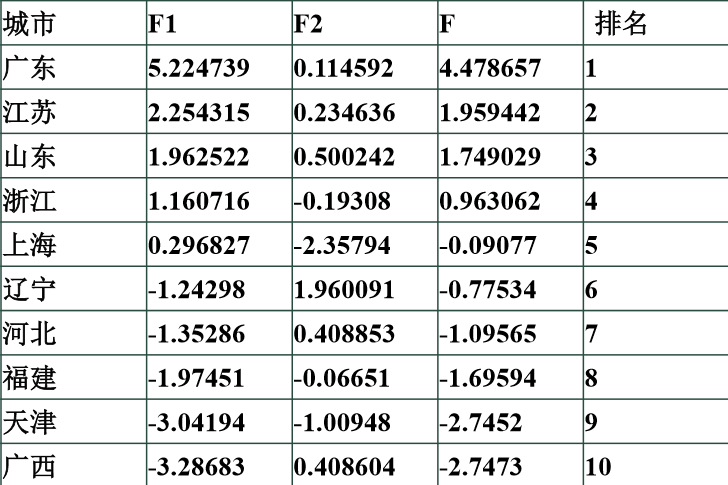
B.附spss的免安装文件地址：

链接：https://pan.baidu.com/s/1euYKvEDu_LevjGweXKVCIw
提取码：u2p8

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请发送邮件至 举报，一经查实，本站将立刻删除。

发布者：全栈程序员栈长，转载请注明出处：https://javaforall.cn/181570.html原文链接：https://javaforall.cn

未经允许不得转载：木盒主机 » 数学建模主成分分析法matlab_主成分分析法建模